By William McCallum
“I’m afraid I can’t explain myself, sir.
Because I am not myself, you see?” Alice in Wonderland.
The idea of equivalence in mathematics is tricky for learners, because when we talk about two things being equivalent, for example the fractions $\frac35$ and $\frac6{10}$, we are emphasizing two contradictory things:
- They are not the same. The numbers are different. If they were the same we would say equal, not equivalent.
- They are the same. Look at the diagram. The shaded parts have the same length and $\frac35$ and $\frac6{10}$ are the same number.
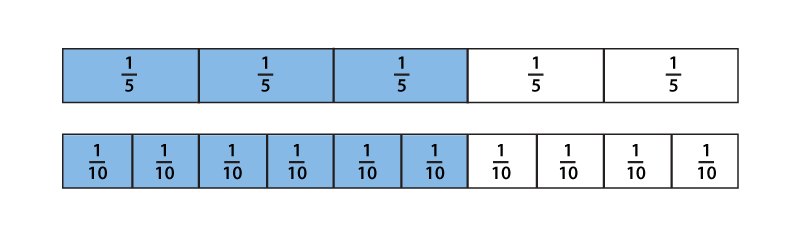
What’s going on here? Really, we are talking about two different things in (1) and (2). In (1) we are talking about the symbolic expressions $\frac35$ and $\frac6{10}$, and in (2) we are talking about the number or quantity they represent. We use the word “fraction” to refer to both the expressions and the number.
When faced with such an ambiguity in language, one way out is to clean up the language. We could, for example, reserve the word “fraction” exclusively for an expression of the form $\frac{a}{b}$, and use the term “rational number” when we want to refer to the number represented by that expression. Such formalism is potentially daunting to students and could get in the way of their learning. And it’s just not the way we speak. Like it or not, we use the same word to refer to both.
Another way to get around the ambiguity is to provide students with a good mental framework into which they can fit the different meanings, making it easier to discern the correct meaning from context. The number line is a good example of this. When we ask students to locate fractions on the number line we are, without making too much of a fuss about it, asking them to perform an act of naming. When they write $\frac35$ above a point on the number line they are putting the expression ($\frac35$) and the number (the marked point) into the same framework. When they write $\frac6{10}$ above the same point they are showing that the same number can have two names.
This is the way equivalent fractions first appear in grade 3, as different names for the same number. It avoids the rigmarole of simplifying or reducing fractions. You don’t need those processes with their accompanying terminology in order to display the visible truth that $\frac35$ and $\frac6{10}$ are different names for the same number. Indeed, the words “simplify” and “reduce” complicate the matter. In everyday language, a simplification of something is actually different from the original thing (think simplified recipe). And when you reduce something you make it smaller. Both words get in the way of the truth. Initially when students work with equivalent fractions they should see equivalences directly, by working with tape diagrams and number line diagrams to see that the numbers indicated by the different fractions are actually the same.
[bctt tweet=”Through students’ work with tape diagrams and number line diagrams, a regularity emerges. – William McCallum, Fractions: Units and Equivalence”]
Students see in both that if they subdivide the thirds in $\frac43$ into two equal pieces, to get sixths, they need to double the number of pieces to get the same quantity, $\frac86$. It always works that way: if they subdivide into $n$ equal pieces they need to multiply the number of pieces by $n$. That is, the fraction $\frac{a}{b}$ is equivalent to the fraction $\frac{n\times a}{n \times b}$, as students learn in grade 4.
This image of equivalent fractions as the same numbers in different units is useful when it comes to adding fractions because it makes sense of the need to find a common denominator. You wouldn’t add 5 centimeters to 3 inches by making 8 centimeter-inches (an imaginary unit consisting of a centimeter followed by an inch). While such a unit of length may sound silly, that same idea is a common error in adding fractions: $\frac52 + \frac34 = \frac86$. (Not.) When students have an image of fractions as numbers on the number line they can see that when they add fractions, they want to measure them in the same units, that is, express them as equivalent fractions with the same denominator, as they do in grade 5.
The idea of equivalence will continue to be important to students, for example when they study equivalent expressions in algebra and congruent figures in geometry. Getting used to the idea that things can be different in one sense but the same in another sense is important in learning to look for and make use of structure.
Next Steps
Can you think of other places in the curriculum where units are important? What role do units play in adding numbers in base ten? How can experience with physical length units prepare students for understanding equivalent fractions?
