Six months ago, I hated trigonometry.
By Becca Phillips
In fact, when my daughter missed a week of school, she announced on her first day back, “Someone has to teach me trig because I missed the whole thing.” Her father jumped in, “That’ll be me. Your mother hates trig.”
At least that used to be true. I have since made peace with my least favorite topic, in large part because of my experiences with the Illustrative Mathematics Geometry course. Let me tell you ways that the IM Geometry course has helped.
The trigonometry unit in the IM Geometry course (Unit 4: Right Triangle Trigonometry) spends several lessons developing the concepts of cosine, sine, and tangent through similar triangles. It has everything I love about IM.
- Using technology to improve access: A Geogebra applet lets students quickly draw similar triangles so the values aren’t lost in the tediousness of drawing everything by hand.
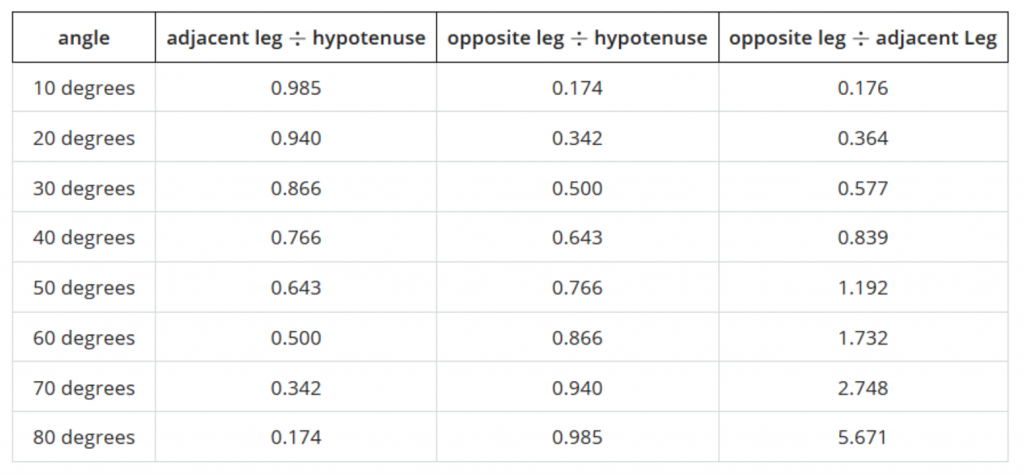
- Student-generated ideas: Once partners have identified consistent ratios within their assigned triangles, they come together to enter the data into a class table and create a class resource. They notice that for all similar right triangles with angles of 10 degrees, 80 degrees, and 90 degrees, the ratio of the adjacent leg to the hypotenuse was approximately 0.985. And 10-80-90 triangles aren’t special: all of these families of similar triangles have their own consistent ratios.
- Notice and Wonder: Using an instructional routine, students infer larger patterns and estimate values for angles not listed. Not only do they learn that every family of right triangles has its own special set of ratios of side lengths, that can be used to solve problems, but they see patterns across the families. What patterns do you notice in the table below?
- Language development: As is so often the case, students build the concept first, examining the ratios and the relationships to the angles, developing the need to identify them with the names cosine, sine, and tangent.
I also like how the table in this lesson builds in increments of 10 degrees and doesn’t just focus on “special” triangles, which can leave students seeing the same numbers (2, ?2, ?3) in a way that can make it harder to see patterns.
The geogebra applet is available here.
I especially love how much time is spent working with the table and not the calculator. I like the way students are asked to work forwards and backwards with values in the table and inferred from the table. For example, students are asked to use the table to calculate the length of the adjacent leg in a right triangle with angles 10 degrees, 80 degrees, and 90 degrees if the hypotenuse of the triangle is 10 units. What row and column would help you answer that question? Why? Students also work backwards and work with data that isn’t in the table. For example, if the ratio of the one leg to the hypotenuse is 0.431, what would be a good estimate for the angles adjacent to that leg? Opposite that leg? What rows or columns helped you answer that? Why?
When I’ve taught this lesson before, I have always skipped straight from similar ratios to the calculator. I might as well have been using a random number generator, for all my students knew. We want students to have sense-making skills (“I asked you the speed of the car, and you weren’t suspicious that the calculator said 10,000 miles per hour?”) but when it came to trig values, I was never even giving them a chance. Through this unit, students spend enough time working in the table to develop their own sense of a reasonable answer before they’re ever handed a device. They see that trigonometric ratios come from measuring real triangles, they notice patterns and trends in the values, and they are the ones to figure out that they can use these patterns to help answer questions without having to do more measuring: a very powerful concept that helps them feel comfortable doing calculations with the values their calculators give them.
One more thing I love about this unit is a small but consequential detail. Let me ask you a question: in the first line of the third paragraph, did your brain stumble when I said “cosine, sine, tangent” in that order? Did you want to correct me? Did you even notice? That order was intentional, and appears in all the tables that the students create as they work through the unit. “Why?” you ask? Because in subsequent courses, they will place (cos A, sin A) on the unit circle and if they’re in the habit of saying cosine, sine, tangent, they won’t miss a beat. I wish that I could reclaim the amount of time I’ve spent in my life reminding myself that the (x,y) aren’t in the “intuitive” order, and I realize now that it’s only “intuitive” because it’s how I was taught. Our students won’t know the difference, and hopefully will have an easier time keeping it straight.
I will admit that I can imagine hordes of parents gesticulating wildly, “What do you mean, you didn’t learn SOHCAHTOA?” but have we really done any damage by omitting it? It has taken some practice on my part to say “cosine, sine, tangent,” but if we let them build the conceptual understanding, let them wait to pick up the calculator, and then let them make up their own mnemonics, they’ll be much better off in the long run…and maybe it won’t take them years to decide that trig isn’t their least favorite topic.
Next Steps
The Illustrative Mathematics Geometry curriculum will be fully released this July. It will be available from IM Certified Partners Kendall Hunt, LearnZillion, and McGraw-Hill, as well as posted to IllustrativeMathematics.org.
