By Kate Nowak
How do we help our students build mathematical understandings that endure past the unit test? If we want students to construct strong, reliable bases of mathematical knowledge, our instruction needs to do more than present explicit procedures—even when that’s done well. Providing lots of opportunities for students to reason can help. So can understanding and leveraging the progression of learning across grade levels. But what does that look like in practice? Let’s examine a single topic in grade 7: solving inequalities.
Suppose that you teach grade 7 math, and by the end of the year you want students to reliably solve an inequality like this and graph its solutions:
$18>3(10-2x)$
So you try the problem yourself, and it looks something like:
$18>3(10-2x)$
$6>10-2x$
$-4>-2x$
$2<x$
$x>2$
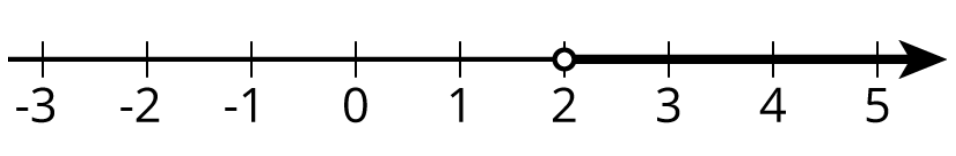
What do students need to be able to do to reliably duplicate what might have gone on in your brain while solving this inequality? Potentially:
- Start solving it like you would solve an equation.
- Remember that if you multiply or divide each side by a negative number, the inequality sign changes from >> to <<, or vice versa.
- Once the inequality is in the form $x>a$, you can graph the arrow pointing in the same direction as the > symbol, but first you have to restate the inequality with the variable on the left, or it won’t work.
Let’s assume they can already solve the equation (the first thing) and now we’re focused on how to get them to do the second two things.
One issue is that problematic conceptions result from this procedural approach to solving inequalities. From the AMS blog: “We define a conception as ‘problematic’ if it describes an understanding that obscures connections to related ideas, introduces mathematical inconsistencies, or is likely to hinder students from developing powerful meanings of future topics.” I’m mainly referring to the third thing, choosing which part of the number line to shade based on which way the inequality symbol is “pointing.” These ideas aren’t meaningfully connected, which becomes obvious when you try to use the same trick to graph $2<x$.
Another issue is that the 3-step process used to solve the inequality is framed as a list of procedures, and if your plan (as mine once was) is that students will all remember those procedures indefinitely without connecting them to understanding, you are going to be disappointed. In the third step, the procedure (draw your arrow in the same direction the inequality symbol is pointing) has its own procedure (make sure the variable is on the left side of the inequality; rewrite if needed). When your procedure has a procedure, you should really rethink what you are doing.
Some people try to demonstrate a procedure and then retroactively make connections to conceptual understanding. These are the folks who think (as I once did) that good teaching is a matter of really clearly explaining. “Here’s why you have to flip over that inequality sign! Chalk and talk and chalk and talk and chalk and talk. See?” Sorry, babe. Cat’s out of the bag. Only half of them were listening and only two of them followed your explanation to the end.
So what should we do instead? Let’s review the progression of these ideas starting back when the kids were still cute. Grade 1 is where they should first encounter the symbols >, <, and =. They should be doing things like “I know that $34$ is greater than $27$, and I can write that like this: $34>27$. If alligators are invoked, I don’t have a problem with that. As mentioned in the progression document for Number and Operations in Base Ten, K–5, using these symbols can be a challenge for young learners, and it can help for them to think of putting the wide part of the symbol next to the larger number. But no worries, there are more chances to use these symbols to compare three-digit numbers in grade 2, fractions with the same denominator or the same numerator in grade 3, multi-digit numbers in grade 4, fractions with different numerators and different denominators in grade 4, decimals to the hundredths in grade 4, and decimals to the thousandths in grade 5.
If students never internalized the meaning of these symbols after all that, you might have to frontload some instruction on it. Hopefully, though, a quick reminder of what the symbols mean will do.
In the pivot to algebra in grade 6, we get variables involved as well as the number line, with these two standards:
- Interpret statements of inequality as statements about the relative position of two numbers on a number line diagram. For example $-3>-7$ means $-3$ is located to the right of $-7$.
- Write an inequality of the form $x>c$ or $x<c$ to represent a constraint or condition in a real-world or mathematical problem. Recognize that inequalities of the form $x>c$ or $x<c$ have infinitely many solutions. Represent solutions of such inequalities on number line diagrams.
In grade 7, there may be unfinished learning related to these ideas from grade 6. If the kids learned that the “direction” of the inequality symbol corresponds to the direction of shading on the number line (but only if $x$ is on the left!), it would help to build some more meaningful schemas. The understanding we want to develop is that on the number line, greater numbers are to the right and lesser numbers are to the left. The symbol $>$ means “greater than” and the symbol $<$ means “less than” (which they have known since first grade). There are no tricks needed (and tricks don’t last in the long run), rather practice at interpreting, comprehending, and writing statements with variables that use these symbols. For inspiration, see IM Grade 6 Unit 7 Lessons 8–10.
Then in grade 7, that understanding is applied to more sophisticated problems. We get the $\le$< and $\ge$> symbols, we have operations on signed numbers so we can solve stuff like $7+y \lt \text-2.5$ and $\text-10 \gt 3x$ and we are solving equations like $3x+7=15$ so we can solve even more complicated inequalities. But let’s focus on how we’re going to tackle that whole “flip the inequality around when you divide by a negative” thing. The answer is, we’re not. This falls into the category of “shortcuts that are perfectly fine if students notice the generalization on their own and reliably use it on their own, but it’s counterproductive to make it the trick we teach everybody.” Instead we’re going to:
- Develop the understanding that the solution to an associated equation gives you the edge or boundary of the solution to the inequality.
- Explore lots of inequalities that represent a context, and reason about what the solution would have to be to make sense in the context. For example, “The inequality $-12x+100?25$ represents an account with $\$100$ in it where someone withdraws $\$12$ each month for $x$ months. They want to maintain at least $\$25$ in the account.” If $x$ is a relatively small number like 1 or 2, they meet their constraint. If $x$ is a relatively large number like 10, they don’t. So the solution should end up saying $x$ is less than some positive number.
- Recognize that the involvement of negative numbers sometimes makes it hard to predict what the solutions will be, and reason about the solutions to relatively simple inequalities using tables and number lines.
- Then put it all together to solve an inequality like $18<3(10-2x)$. Solve the associated equation to determine where the boundary is, and then use any of a variety of strategies to decide whether values less than or greater than the boundary value make the inequality true.
The procedures outlined at the beginning of this post might get some of the students successfully through the exam at the end of the year, even most of them if you are really repetitive about it. But the understanding students develop from an approach that doesn’t introduce problematic conceptions will endure and serve students well throughout their later math coursework and beyond.
Next Steps
Achieving all this understanding doesn’t have to take too long. We offer an approach that takes five lessons in IM Grade 7, Unit 6, Lessons 13–17. Check it out!
