By Vanessa Cerrahoglu and Danielle Seabold, IM Certified® Facilitators
Illustrative Mathematics (IM) believes each student
- has brilliant mathematical ideas
- has experiences and ideas that are valuable
- can make sense of and solve problems
- can learn grade-level mathematics
How can educators act on these beliefs, in teaching and learning with IM 6–12 Math™, to craft learning communities and experiences in which each learner knows, uses, and enjoys mathematics?
Illustrative Mathematics (IM) believes that each student deserves access to grade-level mathematics. Teachers act on this belief when we teach with IM 6–12 Math™ because IM built the curriculum directly from the standards. IM also believes that each student can make sense of and solve problems and has experiences and ideas that are both valuable and brilliant. One way teachers can act on these beliefs is to use the instructional opportunities and strategies offered within each lesson.
This post is the first in a series of three in which we seek to help teachers to
- Highlight instructional opportunities teachers have within IM 6–12 Math™ to enhance access students have to the math. The more we understand these opportunities, the more we notice and use them.
- Be on the lookout for and identify additional opportunities to enhance access and challenge within the curriculum based on students’ strengths. All students can learn grade-level mathematics with the right opportunities and access.
- Prepare and plan for an upcoming lesson with access in mind. We teachers know our students’ strengths and when we plan our lessons with them in mind, we help to remove unnecessary barriers to learning.
We look forward to hearing from you about what resonates with your own experience and how this series may inform your instructional practice moving forward.
Each IM lesson is designed to start by inviting students into the mathematics of the day. Then, activities take students on a deep dive into concepts. Finally, the teacher partners with students to consolidate and apply learning within the activity syntheses, lesson synthesis, and cool-down. Each learner can learn grade-level math with careful, intentional planning.
Within each lesson, how can we enhance students’ access to the mathematical content? What instructional opportunities are already written into the teacher materials? Let’s examine a lesson to find out.
Keeping the Equation Balanced (Grade 8 Unit 4: Linear Equations and Linear Systems] builds towards these learning goals:
- Calculate the weight of an unknown object using a hanger diagram, and explain (orally) the solution method.
- Comprehend that adding and removing equal items from each side of a hanger diagram or multiplying and dividing items on each side of the hanger by the same amount are moves that keep the hanger balanced.
These goals address and build towards 8.EE.C: Analyze and solve linear equations and pairs of simultaneous linear equations.
What does it look like for students to meet these goals? One way to explore what it looks like for students to meet the learning goals of a lesson is to examine the cool-down.
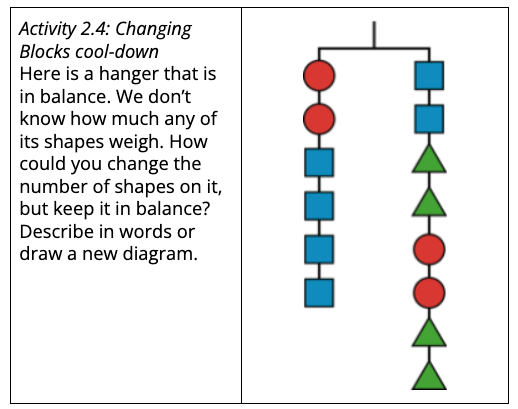
Students might:
- understand that if a hanger is balanced then there is equal weight on both sides, and if a hanger is unbalanced, there is unequal weight on both sides
- know that to keep the hanger balanced, they must add or remove shapes so that the weight remains balanced (equal on both sides)
- understand that identical shapes have the same weight
- find equal-weight shape equivalencies
- describe adding or removing shapes that maintain equal weight on both sides, either in writing or by drawing
So, how does the lesson set students up for success on the cool-down and guide them in meeting the learning goals? It starts with inviting students into the mathematics of the day with the Activity 2.1: Hanging Socks warm-up. This warm-up is designed to activate student thinking around balance and equality.
What do you notice? What do you wonder?

[from Grade 8, Unit 4, Lesson 2: Activity 2.1]
This visual framework for examining balance can enhance access to increasingly abstract representations (hanger diagrams, then equations) later in this lesson and unit.
In this warm-up, and throughout the lesson, students will draw on 3 cognitive functions—conceptual processing, visual-spatial processing, and language—to meet the learning goals. For example, they may rely on
- conceptual processing to understand that if a hanger is balanced then there is equal weight on both sides, and if a hanger is unbalanced, there is unequal weight on both sides
- visual-spatial processing to know that to keep the hanger balanced, they must add or remove shapes so that the weight remains balanced (equal on both sides)
- language to describe, in writing or by drawing, adding or removing shapes that maintain equal weight on both sides
Why does this matter? There are eight ways of thinking, called cognitive functions, that have been found to be integral to learning mathematics. The warm-up calls on three of the eight.
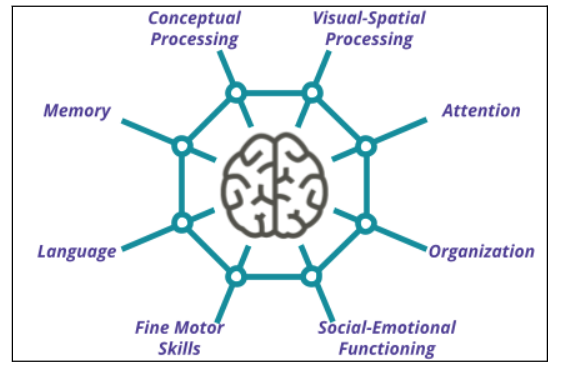
Brodesky et al. (2002). Accessibility strategies toolkit for mathematics. Education Development Center.
When we give our students a mathematical task, we ask them to think in one or more of these ways. When the cognitive functions called upon in a task align to students’ strengths, they are able to more readily and successfully engage with the task. On the other hand, when one or more of the cognitive functions represent a challenge for students, students may encounter barriers to learning and completing the task. In this case, teachers can use the instructional opportunities and strategies offered within each lesson in IM 6–12 Math™ to provide alternate means of accessing the task, without undermining its cognitive demand. (Enhancing access students have to the mathematics is one of the key commitments of the Universal Design for Learning Guidelines outlined on the cast.org website.)
Following the notice and wonder warm-up, students engage with Activity 2.2: Hanging Blocks. The purpose of this task is for students to understand and explain why they can add or subtract expressions from each side of an equation and still maintain the equality, even if the values of those expressions are not known.
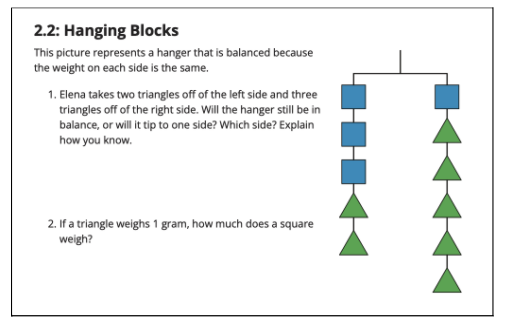
[from Grade 8, Unit 4, Lesson 2: Activity 2.2]
In the next activity, Activity 2.3: More Hanging Blocks, students have the opportunity to solve two more hanger problems and write equations to represent each hanger.
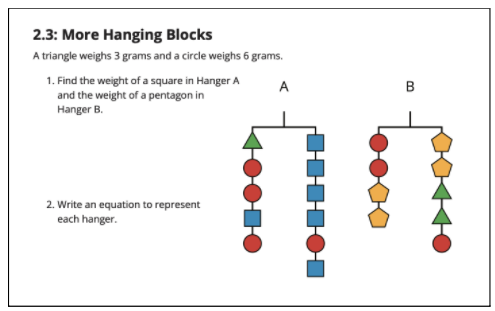
[from Grade 8, Unit 4, Lesson 2: Activity 2.3]
Once again, we may notice that both the conceptual processing and visual-spatial processing cognitive functions are in play. What might this mean for students? If conceptual and visual-spatial processing happen to be cognitive strengths for students, they might experience this task joyfully as they tinker with important mathematical concepts. On the other hand, if these cognitive functions present students with a challenge, we teachers have an opportunity to enhance access students have to conceptual and visual-spatial processing so that they too may experience joy and confidence in tinkering with the mathematics of the task. Upon reading the embedded instructional support, we have some instructional decisions to make. Let’s examine some of these options.

Let’s focus on Hanger A. How might we simplify it in a way that students will engage with the same learning? Is there a way to simplify it so that students will also get the same answer as their classmates? Based on the suggested instructional strategy, we could simplify Hanger A in several ways as illustrated below:

Which of these options can enhance access students have to the mathematics, attend to the cognitive functions in play, and build to the learning goals of the lesson? Let’s think back to the second learning goal of the lesson: Comprehend that adding and removing equal items from each side of a hanger diagram or multiplying and dividing items on each side of the hanger by the same amount are moves that keep the hanger balanced. If we choose Option 1, we remove an opportunity students have to tinker through adding or removing equal items from a hanger. So, what are the impacts to learning if we choose Options 2 or 3? We recognize that both Options 2 and 3 ensure students tinker with adding or removing equal items from a hanger while giving students the opportunity to strengthen their ability to internalize comprehension. Upon closer inspection, we can see that Option 3 will yield the same value for the blue square as peers working on the original hanger. Option 3 will serve to foster a sense of community across the classroom.
Why not use the simplified hanger for everyone? The original hanger foreshadows future lessons, where students add or subtract both constants (circles) and variables (squares) from both sides of the equation. Use of a simplified hanger might meet today’s objectives, yet it could affect the overall progression of learning for the unit. Great care must be taken when making accommodations to enhance access. The use of a carefully selected, simplified hanger, along with other instructional moves, will enhance student access to grade-level work as they build the conceptual underpinnings of analyzing and solving linear equations.
Next Steps
As you prepare for an upcoming lesson, we invite you to
- look and listen for cognitive functions that are strengths in each of your students
- reflect on the mathematical focus of the lesson as evidenced in the learning goals and cool-down
- identify the intended cognitive functions of each task
- consider the impact of instructional decisions and task accommodations on your students’ ability to meet the learning goals
Please be on the lookout for the next entry in this series, and share insights gained by going through this process. We’d love to learn from you.
