By Dr. Kristen Taylor, IM Certified® Facilitator
Math teachers can talk all day about math! We get super excited when we encounter someone else who enjoys these conversations as well.
But too many of our students don’t get to experience that joyful discourse, which limits their understanding of and positive experiences with math.
How would our students’ math learning and perception about math improve if they also had regular opportunities to talk about math? How might these opportunities help us create a world where learners know, use, and enjoy mathematics?
That’s where math language routines (MLRs) come in. Embedded in IM® K–12 Math, these routines are designed to give all students opportunities to reason, communicate, and deepen their understanding in collaborative and supportive ways.
What are math language routines?
The Understanding Language/Stanford Center for Assessment, Learning, and Equity (UL/SCALE) at the Stanford Graduate School of Education developed eight math language routines (MLRs) to help teachers “amplify, assess, and develop students’ language” in the math classroom.
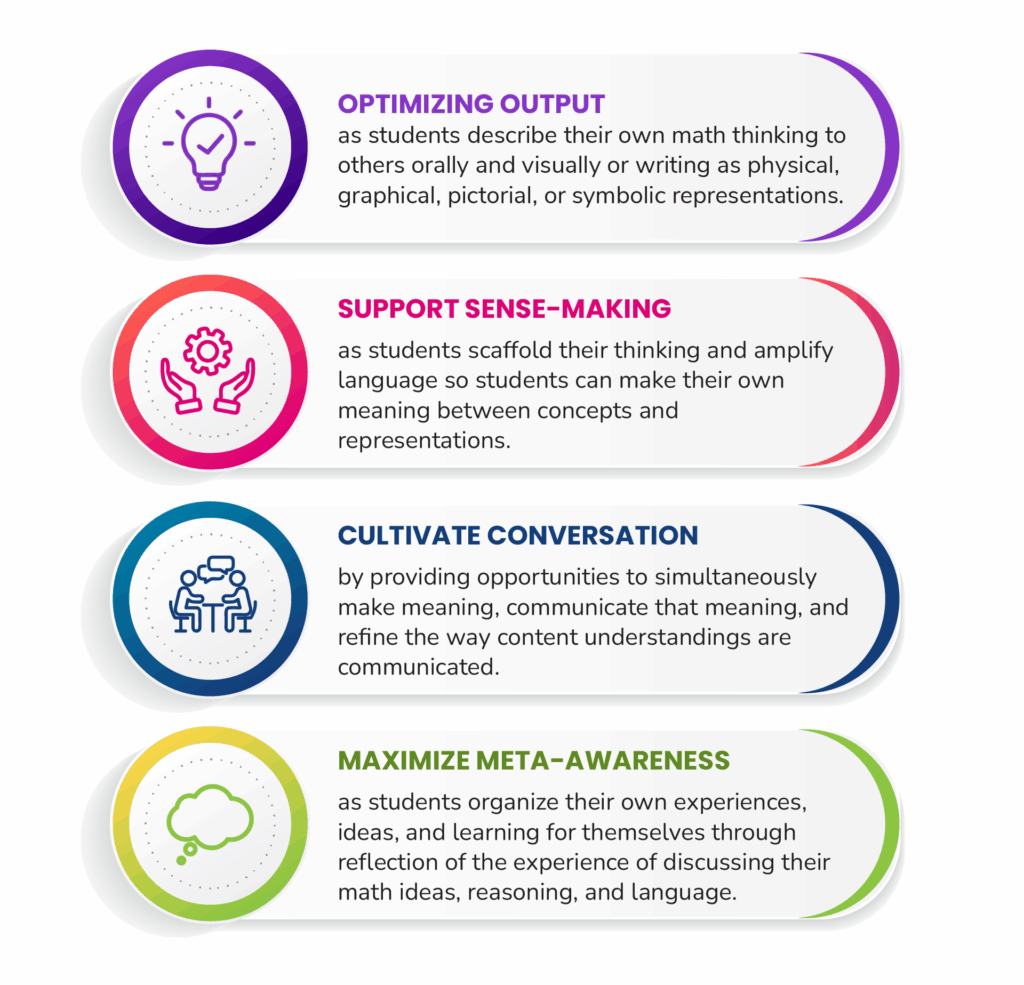
Each routine is grounded in four design principles that invite students into meaningful math discussions and create opportunities for deeper learning.
MLRs support students in advancing their thinking in the following ways:
This doesn’t just mean that teachers tell students to talk about math and they do. We know that if we simply open the space and tell students to talk, much of the discussion will veer off-topic. Math language routines help teachers create a structure in which students can bring those four design principles to life.
Let’s explore how each MLR supports students in developing their mathematical thinking and engaging with the Standards for Mathematical Practice.
MLR 1: Stronger and Clearer Each Time – Students begin by writing a response to a math problem, then verbally share their response with a partner to receive feedback. They use this feedback to revise and strengthen their original written response.
This MLR encourages students to reflect on their own thinking and consider the perspectives of others. Students practice giving, receiving, and applying constructive feedback while developing their listening skills. Repeated review and revision help students communicate their mathematical reasoning with greater clarity, precision, and focus.
(This connects to Standards for Mathematical Practice 1: Make sense of problems and persevere in solving them, 3: Construct viable arguments and critique the reasoning of others, and 6: Attend to precision.
As students verbalize and review in writing the strategies they used and the justification of those strategies, students have the opportunity to get feedback which can be used to critique the precision of their solution strategy and answer.)
MLR 2: Collect and Display – Students engage with their own and others’ mathematical ideas as the teacher captures and displays their language, strategies, and reasoning—using written words, diagrams, or pictures—during partner, small group, or whole-class discussions.
By recording student thinking in real time, the teacher creates visible and lasting representations that support deeper engagement. These shared visuals help students clarify their own communication, build on one another’s ideas, and revisit key concepts in future discussions. They can reference mathematical vocabulary, make connections between ideas, and strengthen their understanding over time. This MLR supports visibility of student thinking and fosters a sense of ownership over mathematical learning.
(Standards for Mathematical Practice 3: Construct viable arguments and critique the reasoning of others, and 6: Attend to precision.
As students view the thinking of their classmates, they can address any differences they see between their representation and their classmates’ representation, further pushing students to find the most efficient or precise representation to solve the problem.)
MLR 3: Critique, Correct, and Clarify – Students rewrite a math response from an example that is incorrect, incomplete, or otherwise ambiguous.
In addition to providing students with a space to further engage in math, students employ a “growth mindset” and consider revisions to their work in order to strengthen their communication. This MLR helps students “try on” others’ math thinking in order to improve it.
(Standards for Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Students have the opportunity to engage with a strategy for solving that might be different from theirs in order to find ways to improve the situation representation, address and clarify misconceptions about the math, and “borrow” parts of the strategy that were relevant to add to their toolbox.)
MLR 4: Information Gap – In this routine, each student in a group receives different pieces of information about a math context. Together, they collaborate—through oral and/or visual communication—to combine their pieces and bridge the gap between the given information and the question to be solved.
As students work to make sense of their individual contributions, they also determine what additional information is needed to fully understand and solve the problem. This encourages purposeful collaboration, as students share, question, and clarify information while considering the most efficient strategies. This MLR supports meaningful exploration of mathematical contexts and promotes problem-solving driven by curiosity and need-to-know.
(Standards for Mathematical Practice 2: Reason abstractly and quantitatively, and 4: Model with mathematics.
As students imagine the kinds of information they need to know and explain why they need to know that information, they are building an understanding of the problem and possible solutions.)
MLR 5: Co-Craft Questions and Problems – Students are given either a mathematical answer or a context and are invited to create a question or problem that could lead to that answer or be solved using that context.
With this MLR, students use their creativity to explore a math context as they iterate their understanding in order to identify questions that can be asked and answered by the context. As students share their understandings with others, they also uncover the importance of slowing down to explore and think before they try to answer a question.
(Standards for Mathematical Practice 4: Model with mathematics.
By creating their own questions and problems, students learn to visualize the parameters of the problem as they consider what kind of answers are possible with the information provided.)
MLR 6: Three Reads – Students read a math problem three times, each with a distinct purpose and a brief discussion between each read.
This routine encourages students to slow down and make sense of the problem before jumping to a solution. With each read, they focus on: (1) understanding the context, (2) identifying the mathematical relationships, and (3) considering possible strategies to solve the problem. By intentionally engaging with the problem in stages, students deepen their comprehension and become more aware of their own thinking. This MLR supports metacognitive problem-solving and helps students develop a more thoughtful, intentional approach to math.
(Standards for Mathematical Practice 1: Make sense of problems and persevere in solving them.
As students set a purpose for reading each of the three times, students practice and see the importance of understanding the problem context and using the information they know from the problem in order to identify a strategy for solving.)
MLR 7: Compare and Connect – Students identify, compare, and contrast their own understandings with other students’ mathematical approaches, representations, concepts, examples, and language.
As students encounter other’s math thinking, this MLR opens the floor for students to interact with each other’s thinking and consider how they see and talk about math.
(Standards for Mathematical Practice 4: Model with mathematics, 6: Attend to precision, and 7: Look for and make use of structure.
As students find differences and similarities between their strategies for solving, they mine their understanding of the math concept in relation to the structure and steps of another student’s understanding of the math. This allows students to attend to precision because to be understood by another, they have to be precise with their explanation.)
MLR 8: Discussion Supports – Students engage with strategies through multiple modes—such as visuals, audio, movement, and symbols—to better make sense of complex language, ideas, and classroom communication.
These multi-modal supports enhance access to mathematical concepts, allowing students to build understanding while also strengthening their ability to communicate mathematically. This MLR helps students deepen their conceptual knowledge and express their thinking in a variety of meaningful ways.
(Standards for Mathematical Practice 1: Make sense of problems and persevere in solving them, 3: Construct viable arguments and critique the reasoning of others, 5: Use appropriate tools strategically, and 6: Attend to precision.
Using discussion supports helps students to see the reasoning of others as well as identify which tools to solve are most appropriate.)
Conclusion
At Illustrative Mathematics, we believe every student deserves access to rich, meaningful math learning—and language plays a critical role in that journey. By intentionally structuring discourse with purpose, MLRs bring IM’s core beliefs to life: that students learn math by doing math, that their ideas matter, and that everyone can grow in their mathematical thinking.
Next Steps
For more information on MLRs, view the original paper from Stanford University: Principles for the Design of Mathematics Curricula: Promoting Language and Content Development.
Want to explore IM’s problem-based curriculum further? Visit AccessIM.org and create a free account.
 By Dr. Kristen Taylor
By Dr. Kristen Taylor
IM Certified® Facilitator
Dr. Kristen Taylor has been a teacher, instructional coach, curriculum coach, assistant principal, and a principal in urban districts and charter schools. She has supported teachers at all levels from PK–12 and administrators at grades PK–8.