By Lisa Matthews, IM Certified® Facilitator and PL Specialist Team for Grades 6–12
The IM curriculum is so thoughtfully designed and written that even those of us who have spent years with IM often find content that is new, or ideas within it that deepen our math teaching practice. Maybe it’s a way to amplify mathematical language with the Math Language Routines, or a more robust understanding of the coherent progression of representations. This blog post highlights a piece of the IM 6–8 curriculum that may be brand new to many of us: Unit 9.
What does it mean to Model with Mathematics?
What are Unit 9s about? Like everything in IM, it starts with the Standards, in this case, Math Practice 4 (SMP 4). The IM Curriculum is aligned to both the CCSS-M Content Standards and The Standards for Mathematical Practice (Math Practices). Math Practice 4 in the CCSS-M is Model with Mathematics, and states:
Mathematically proficient students can apply the mathematics they know to solve problems arising in everyday life, society, and the workplace. In early grades, this might be as simple as writing an addition equation to describe a situation. In middle grades, a student might apply proportional reasoning to plan a school event or analyze a problem in the community. By high school, a student might use geometry to solve a design problem or use a function to describe how one quantity of interest depends on another…
To summarize: “In the Standards, modeling means using mathematics or statistics to describe (i.e., model) a real-world situation and deduce additional information about the situation by mathematical or statistical computation and analysis.” (Learning Progressions)
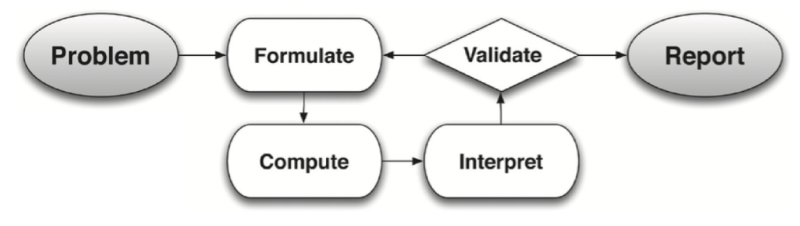
Modeling is considered so important that it’s a domain in the CCSS-M high school standards. (If Modeling is new to you, check out this IM Certified Blog post by Kate Nowak.) It is expected to be taught alongside all the other content standards, and because modeling is about specific mathematical ideas, there are content standards suggested for students to use for making mathematical models, indicated by a star symbol (*). The high school modeling cycle (Figure 1) begins with students identifying the problem they are solving, then formulating a plan to approach the problem. Next, students follow the plan to compute their answer and interpret the result. Then, they validate their response. If it makes sense they report their answer, and if not, they formulate a new plan and continue the cycle.
Mathematical Modeling in IM K–8 Math
As mentioned in Math Practice 4, the modeling that students will do in high school needs to be supported by experiences that students have had with modeling in elementary and middle school. The IM curriculum provides students with opportunities to model with mathematics and apply their mathematical problem solving skills to real-world situations throughout K–8 (see Table 1).
Table 1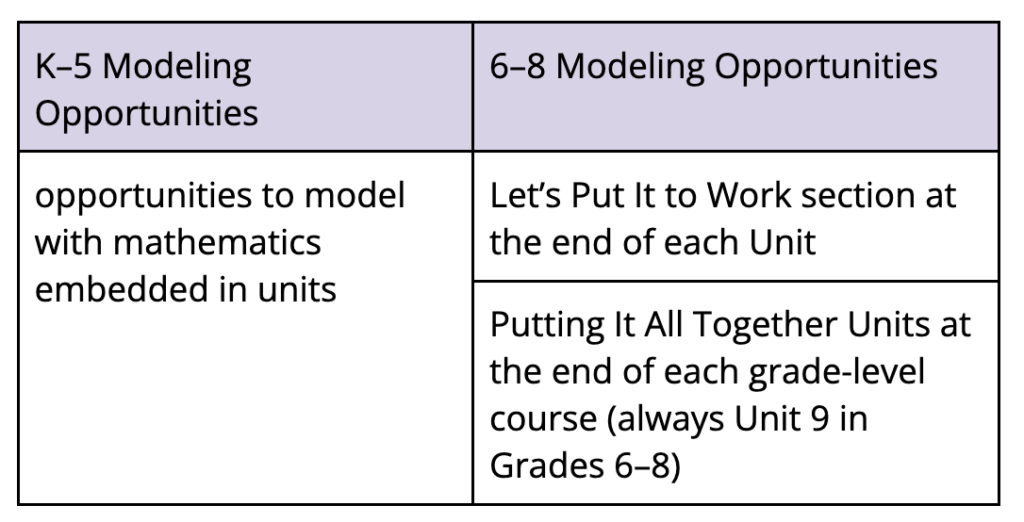
And that brings us back to our hidden gems! Unit 9s in Grades 6–8 contain explicit modeling problems that are designed to give students authentic, grade-level experiences with parts of the Modeling Cycle. Unit 9 in Grades 6–8 contains explicit modeling problems that are designed to give students authentic, grade-level experiences with different parts of the Modeling Cycle so that students can say, “I can model with mathematics!”
Learning Targets for Modeling with Mathematics
But what do those kinds of modeling experiences look like? How do we build students’ capacity to model with mathematics over the elementary years, and into the middle grades, and then into high school?
These statements from Math Practice 4 give us some concrete examples of the kinds of mathematical work students in 6–8 can do to model with mathematics. These learning targets come from IM 9-12 Math:
- I can make assumptions and approximations to simplify a complicated situation.
- I can articulate which questions are essential to answer to solve a problem.
- I can identify and collect or estimate missing information needed to solve a problem.
- I can relate important quantities using a mathematical model, such as an equation, table, or graph.
- I can use a mathematical model to draw conclusions about a situation.
- I can interpret and report on the results of a model in the context of the situation.
- I can refine or revise the model to more accurately describe the situation.
- I can explain the limitations of my model.
Mathematical Modeling in IM 6–8 Math™ v.III
IM has taken this modeling work and organized it into 3 aspects of modeling in Unit 9s, and students engage in these 3 aspects of modeling at different levels:
- Collecting and Selecting Information
- Formulating the Model
- Processing Information
Here’s an example from Grade 6 Unit 9 (Figure 2):
Figure 2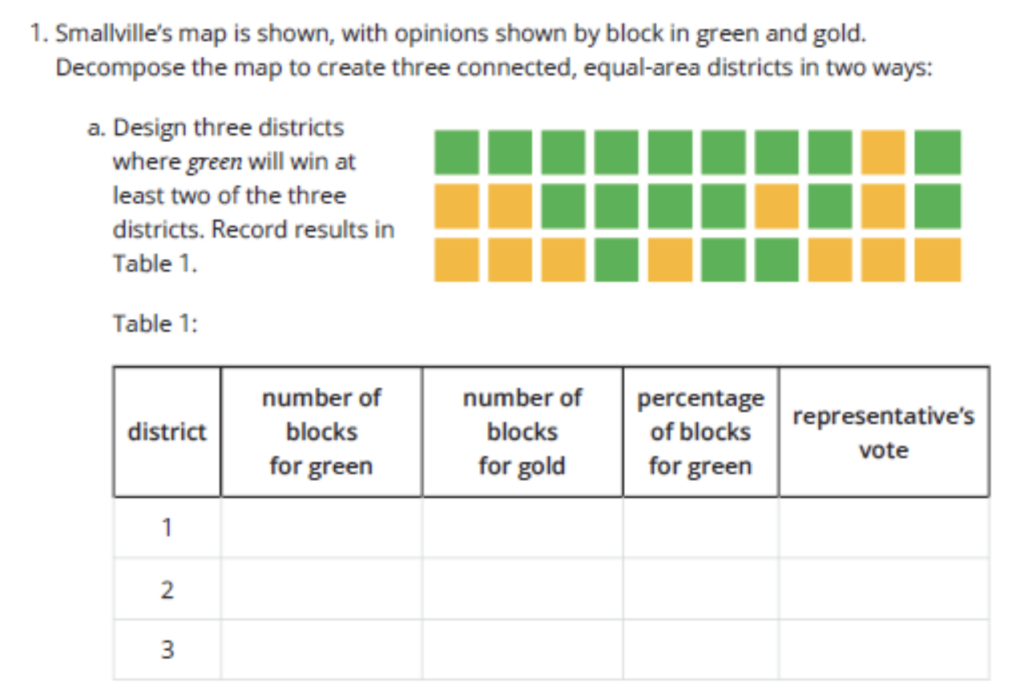
(Find this lesson on the IM Curriculum demo site)
In this activity, students are asked to “gerrymander several districts: to divide it into sections in two ways to influence the final voting result in opposite ways. The mathematics here involves geometric properties of shapes on maps: area and connectedness, as well as some proportional reasoning.” [From IM Grade 6 Unit 9 Lesson 6 Narrative] The IM curriculum authors designed this task as an opportunity for students to begin working on Processing Information, where the collecting, selecting, and formulating have been included in the structure of the task. You could consider this kind of task an opportunity to dip your toe into the Modeling Cycle pool.
In contrast, here is an example from Grade 8 Unit 9 (Figure 3):
Figure 3

In this activity, students investigate whether temperature is a function of latitude. Here the students must first make decisions about what information will be useful in answering their question, weigh the pros and cons of each model, and make a choice themselves. Later in the lesson students will reflect on why some of this information may not be useful, consider more useful information, and then reflect on how they might process the information that is generated.
All of the tasks in Grade 6–8 Unit 9s are written with various levels and combinations of the 3 Aspects of Modeling so that students are starting to learn some swimming fundamentals in the Modeling Cycle pool. For middle school, that’s the goal—to prepare students to go swimming in the deep end when they get to high school.
Consolidate and Apply: How to use IM 6–8 Math v.III modeling tasks
Now that you know about these opportunities for middle school students to model with mathematics, you may be lamenting that these modeling opportunities are in Unit 9, and we all know that pacing can be a challenge. You may be worried that you won’t get to Unit 9 and your students will miss out on modeling.
That’s the beauty of these modeling tasks, though: You don’t have to wait! The lessons and tasks in Unit 9 are designed to be done only after certain content has been learned. For example, in Grade 8, the first 3 modeling lessons can be done anytime after Unit 1, and the last 3 lessons can be done anytime after Unit 6. Each grade level is slightly different, so Table 2 gives a summary of each Unit 9, when the tasks are appropriate, and approximately how long they will take.
Modeling tasks and lessons are also flexible, and can be used in different ways, including:
- during exam week
- after state testing
- before holidays when you don’t want to start a new unit
- when a fair chunk of your class is absent (e.g., the band leaves after lunch)
- as a project for individuals or small groups
- depending on the class community and on the challenge of the task, maybe when you’re gone!
What’s important to remember is that all our students need opportunities to engage with the different aspects of the modeling cycle before they get to high school. This might not mean that every student gets to engage with every lesson, but that they have a variety of opportunities throughout their K–8 experience. How you decide to use them to meet the needs of your students is up to you! We have included a table (see Table 2) so you can get an overview of what each Unit 9 contains, when the lessons can be taught, and how long each lesson or group of lessons will take.
If we have piqued your curiosity about what it’s like to swim in the deep end of the High School Modeling Cycle pool, please consider reading the following blog posts, as well as checking out some of the IM Modeling Prompts in Algebra 1, Geometry, or Algebra 2:
What does it mean to use mathematics? by Dr. Bill McCallum
Making authentic modeling possible by Kate Nowak
Next Steps
If this post helped you find a hidden gem in IM, or if you have been using Grade 6–8 Unit 9s with your students, we would love to hear your stories and see examples of how Unit 9s are creating authentic opportunities for your students to model with mathematics in Grades 6–8! Please consider sharing on twitter using the hashtag #LearnWithIM, or on instagram tagging @IllustrateMath.
