By Brianne Durst
Grade 1 teachers have the awesome responsibility of introducing their students to, and helping them build an understanding of, the structure of our number system. This is no small task! Just think about how many tasks in later years depend on an understanding of place value. This understanding that begins to develop in grade 1 is the foundation of number sense.
So, how should we begin students’ journey to understanding place value? We want to build on students’ prior learning and give them sufficient time and experiences to extend and solidify their understanding. Grade 1 does this by following the Invitation-Deep Dive-Consolidation/Application structure of the IM curriculum.
Extending an Invitation in Unit 1 (Adding, Subtracting, and Working with Data)
Unit 1 Section A is an invitational welcome for both students and teachers.
Students are invited to get to know one another and experience joy in their new math community by playing games that focus on addition and subtraction within 10, something familiar from kindergarten. Beginning the year with fun, low-stakes activities can quell nerves that students may have as they enter a new school year. This can go a long way in creating a math community where all students feel capable, comfortable sharing ideas, and valued as an important member of the community. Unit 1 Section A also launches the year-long work of developing fluency with addition and subtraction within 10. Giving students time to work with these smaller numbers helps set them up for success with what is to come in later units.
Section A is an invitation to teachers to learn about the students in their new class in an authentic way. As teachers, we start a school year eager to get to know our students as mathematicians. While students play games, the teacher has time to listen to students explain their ideas and reasoning. Through observation and conversation, teachers learn a lot about their students as mathematicians and how they are working with numbers through 10. The data work in Sections B and C allows for continued community building as students learn about each other as they create surveys and representations of class data. They ask and answer questions about their data, continuing their work with addition and subtraction within 10. Future learning will be built on these understandings.
Building onto the Foundation in Unit 2 (Addition and Subtraction Story Problems) and Unit 3 (Adding and Subtracting Within 20)
In unit 2, the focus shifts to making sense of and solving different types of story problems. The numbers used in the problems are intentionally kept within 10 to allow students to continue to build fluency with addition and subtraction in this range.
Then, Unit 3 Section A offers students the chance to assess their fluency within 10 and identify any facts they need to continue working with to become fluent. Through this work from the beginning of grade 1, students develop a strong foundation on which to build.
What would be helpful to know about place value to find the value of this sum?
37 + 25
The expression above is one that students will encounter in Unit 5. Asked to find the value of this expression in the beginning of grade 1, students may count out 37 cubes and 25 cubes and count them all to find the total. Others may start with 37 and count on 25 more. Neither strategy is very efficient when working with these numbers, but both are reflective of the work first graders have done up to this point.
In kindergarten, students worked with teen numbers and saw that all teen numbers have 10 and some more. Without labeling them, kindergarteners were working with groups of 10 ones. In Unit 3 Section B, first graders build on this work and learn that the group of 10 ones makes a new unit called a ten. They continue working with teen numbers and see that each teen number has 1 ten and some more ones. Throughout this work students see teen numbers represented on double 10-frames. This representation allows students to see both the unit of ten, and the 10 ones inside that unit. This is essential as students develop a true understanding of the unit of ten.
In grade 1, students have their first experiences using place value to add and subtract. They add and subtract teen numbers and one-digit numbers, beginning with expressions that will not require making a new unit of ten, such as 14 + 3 or 12 + 5. They notice that the unit of ten doesn’t change, and relate the sum to adding and subtracting of ones.
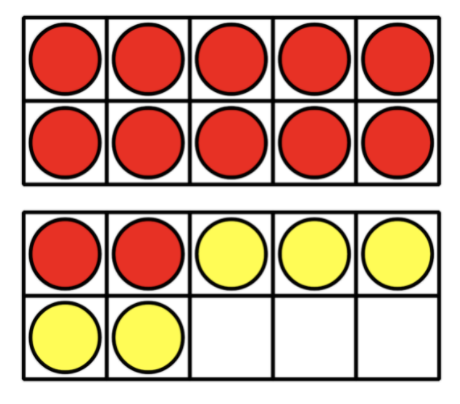
Students then progress to adding and subtracting teen numbers and one-digit numbers that will require making a new unit of ten or breaking apart the unit of ten. Students rely heavily on their previous work with numbers within 10 to support them in finding the value of these sums and differences.
How do both of these strategies rely on fluency with numbers within 10?
Diego is playing Number Card Subtraction.
He started with 15 and then picked an 8.
He started out by doing this:
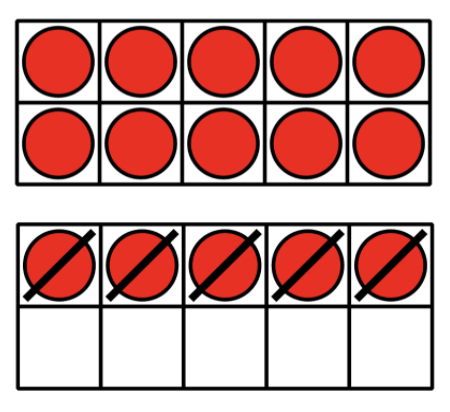
What could Diego do next to find the difference?
Andre was also finding the value of 15 – 8.
He started out by doing this:
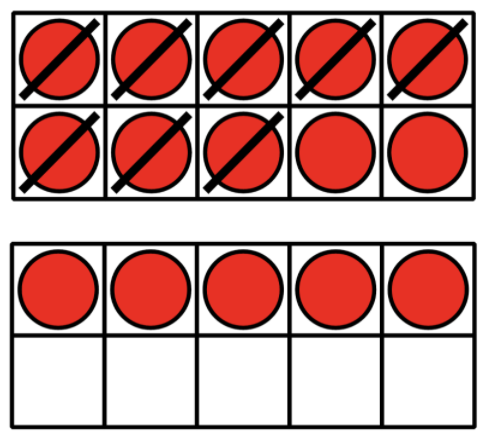
What could Andre do next to find the difference?
Deep Dive into New Learning in Unit 4 (Numbers to 99) and Unit 5 (Adding within 100)
In Unit 4, students use what they have learned about teen numbers and the unit of ten to generalize the structure of two-digit numbers, relating the two digits to the number of tens and ones. They interpret and use multiple representations of numbers up to 99, such as connecting cubes, base-ten diagrams, words, and expressions. Connecting cubes in towers of 10 and singles are used throughout grade 1, rather than base-ten blocks, so that units of ten can be physically composed and decomposed with the cubes.
Although students work physically with connecting cubes, they interpret base-ten diagrams, recognizing the diagram as a simplified image of the connecting cubes. This helps students make sense of a more efficient way of drawing diagrams to match their connecting cubes. As students develop their understanding of place value and work with each of these representations, they are able to compare any two-digit numbers by comparing the number of tens, and, if needed, the number of ones.
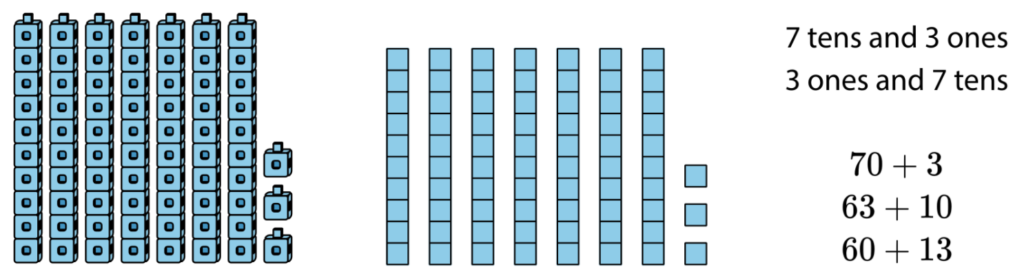
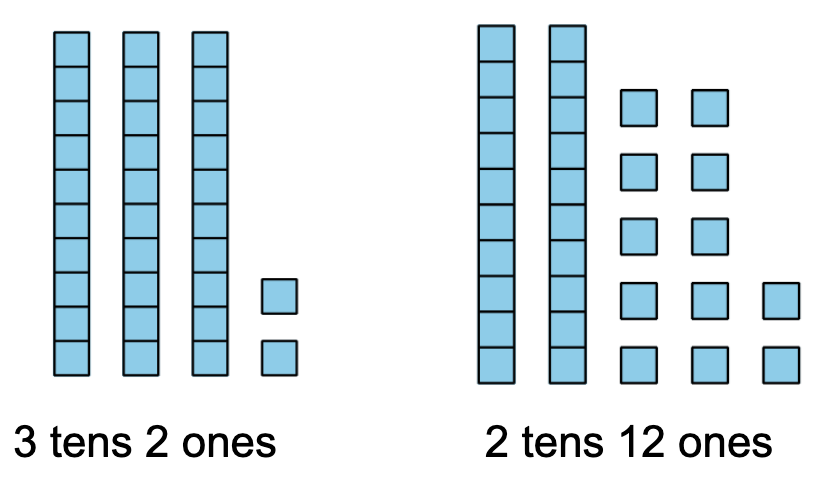
In Unit 5 students will add 2 two-digit numbers that require making a new unit of ten. In preparation for this, students interpret and build two digit numbers with different amounts of tens and ones. For example, students learn to recognize 32 as both 3 tens 2 ones and 2 tens 12 ones.
Students then begin adding within 100 following a similar learning progression. They add 2 two-digit numbers that do not require making a new unit of ten, such as 42 + 35. They use their place value understanding to add tens and tens and ones and ones, or add on adding tens first then ones.
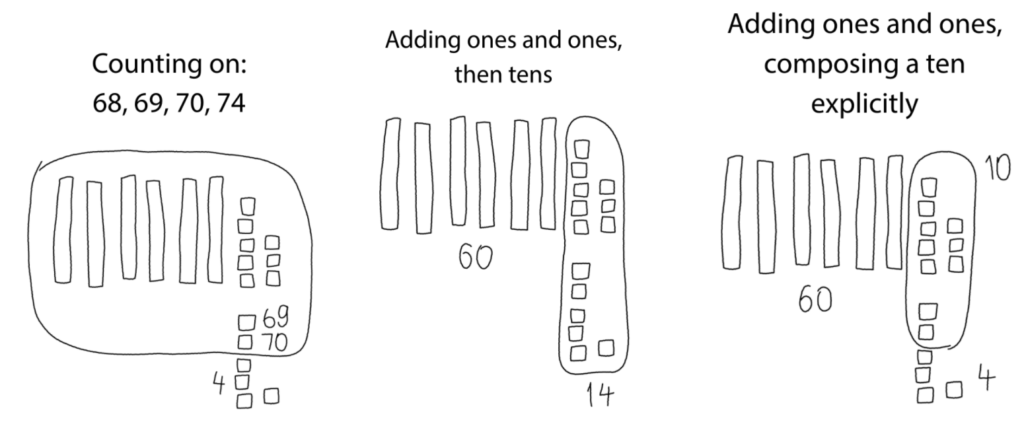
Next, students add a two-digit and a one-digit number that requires making a new unit of ten, such as 68 + 6.
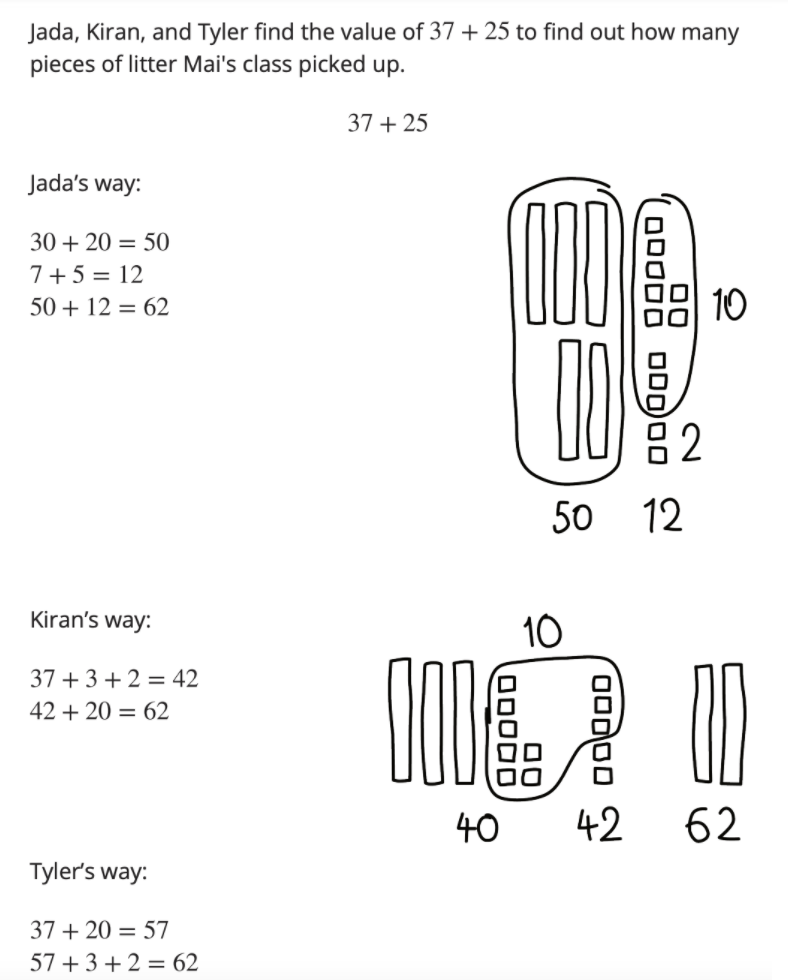
Now, we are ready to come back to the expression presented earlier: 37 + 25. Students are now equipped to add within 100 in more efficient ways. They discuss different strategies based on place value, such as adding tens and tens and ones and ones. They might add on to make a new ten, then add the rest. Students represent their thinking using connecting cubes in towers of 10 and singles, base-ten drawings, and equations.
Mai and her classmates volunteer to clean up the local park.
They pick up 37 plastic bottles and 25 paper wrappers.
How many pieces of litter did they pick up all together?
Consolidate and Apply Learning in Unit 6 (Length Measurements Within 120 Units)
According to standard 1.NBT.A.1, students should count to 120, read and write numbers in this range, and represent a number of objects in this range with a written numeral. Working toward this standard allows students to apply their new understanding of place value.
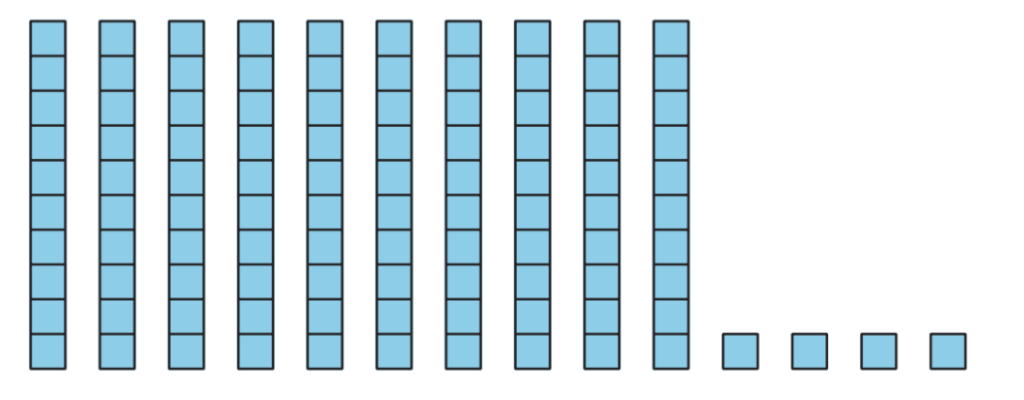
While the focus on linear measurement in Unit 6 may feel unrelated to the place value work in the previous units, it is actually a wonderful opportunity to consolidate and apply this learning. After learning proper measurement techniques, students use base-ten cubes to measure lengths up to 99 length units, then measure lengths even longer than 99 length units. In order to determine the total number of length units, they organize the cubes into groups of 10. They see that 10 tens is 100. A hundred is not discussed as a unit in grade 1, but the written notation is introduced so students can read and write the numbers 100–120.
10 tens 4 ones is 104.
Grade 1 teachers have the awesome responsibility of introducing their students to, and helping them build an understanding of, the structure of our number system. The IM Grade 1 materials support teachers in doing this by taking time to build the necessary foundational skills and strategically building upon and applying these skills.
Next Steps
Consider the work you do to help students build an understanding of place value. In what ways do you support building on foundational skills to allow for a strong conceptual understanding of the base-ten structure of numbers?
Check out the entire Stories of Grades K–5 blog post series:
Story of Kindergarten
Story of Grade 1
Story of Grade 2
Story of Grade 3
Story of Grade 4
Story of Grade 5
You can also download IM’s Stories of Grades K–5 free ebook!
