By Patti Drawdy and Yenche Tioanda
“Why not start the year with place value?” Kaneka Turner, Grade 4 Lead Writer, hears this question often. Isn’t making sense of and operating on large numbers pretty essential in grade 4? Indeed, they are. Yet students begin Grade 4 in IM K–5 Math by playing with rectangles. In the first few lessons, they use square tiles to build rectangles of certain side lengths or areas. Why?
The Invitation to Grade 4 Math
As in all IM courses, the flow of units in Grade 4 was considered with care—with both the mathematics and the students in mind. And as is typical with an IM course, Grade 4 opens with an invitation: to play, observe, and engage with content that is both relatable and fresh, and that improves students’ access to the major work of the grade. The opening unit also strives to generate conversations—around ideas, ways of thinking, and the experiences of the thinkers. These conversations serve as a basis for building a positive and inclusive learning community, an integral part of all first units IM K–5 Math.
The exploration of rectangles in the opening unit, Factors and Multiples, follows the design principles above. It activates concepts of multiplication of whole numbers and area of rectangles from grade 3. Then, it prompts students to make new observations about the relationship between pairs of side lengths and area, which paves the way for the introduction of factor pairs and multiples. The geometric context is also purposeful in that it grounds prime and composite numbers in concrete representations before students make sense of such numbers in situations that require more abstraction.
The experiences here develop students’ multiplicative reasoning, allowing a wider range of learners to access upcoming work on fraction equivalence.
From Factors and Multiples to Fraction Equivalence
The work in Unit 2, Fraction Equivalence and Comparison, also builds ideas introduced in grade 3: the size of fractions, the location of fractions on a number line, and equivalent fractions. They use these insights to compare and order fractions with denominators 2, 3, 4, 5, 6, 8, 10, 12, and 100.
Students continue to engage in multiplicative reasoning. They explore doubling and halving—first by repeatedly folding strips of paper in half, which doubles the number of equal parts with each fold, and then by halving the parts in tape diagrams, which creates twice as many parts and smaller unit fractions. Later, they partition segments on tape diagrams and intervals on number lines into other numbers of equal parts. Such repeated reasoning allows students to more readily relate fractions in which one denominator is a multiple of another denominator and to see fraction equivalence.
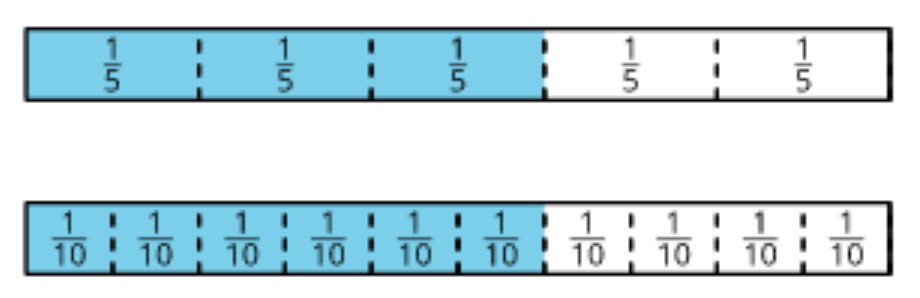
IM K–5 Math: Grade 4 Unit 2 Overview
Partitioning a diagram into equal parts becomes increasingly inconvenient as the denominator gets larger. It’d be easy enough to partition a number line into, say, 10 parts, but unwieldy to partition one into 100 parts. This practical limitation motivates a need for generalization, which supports students in relating tenths and hundredths. Understanding of factors and multiples also comes into play as students generalize the process of partitioning a number line to identify equivalent fractions.
Opportunities to strengthen fluency with multiplication are present not only in the core activities but also in the warm-ups, as shown in this sampling of Number Talks from the first two units. The numbers in each sequence encourage students to apply the distributive and associative properties to mentally find the value of each expression.
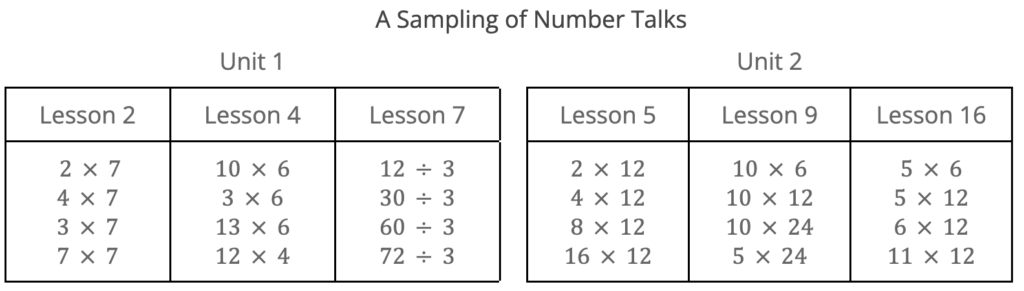
New Numbers, Familiar Operations
Having spent time deepening their understanding of the size of fractions, students are now better equipped to see—more abstractly than in grade 3—how fractions can be composed and decomposed, and like whole numbers, be added, subtracted, and multiplied. This work happens in Unit 3, Extending Operations to Fractions.
In grade 3, students saw multiplication in terms of equal groups of whole numbers. Here, they extend that insight to include equal groups of fractional amounts. Through repeated reasoning with diagrams and equations, students see regularity in the product of a whole number and a fraction, namely, that a fraction $\frac{a}{b}$ is $a\times \frac{1}{b}$, and that $n\times \frac{a}{b}$ gives $\frac{n\times a}{b}$.

IM K–5 Math:
Grade 4 Unit 3 Overview
Grade 4 Unit 3 Lesson 4 Synthesis
Everyday contexts are used to help students make sense of non-unit fractions as products and sums. For instance, in the context of using only $\frac{1}{4}$-cup and $\frac{3}{4}$-cup measuring cups to measure the ingredients in a recipe, $\frac{5}{4}$ can be understood as a product (5 x $\frac{1}{4}$, or using the $\frac{1}{4}$-cup 5 times), a sum of unit fractions with the same denominator ($\frac{1}{4}$+$\frac{1}{4}$+$\frac{1}{4}$+$\frac{1}{4}$+$\frac{1}{4}$, or repeatedly adding $\frac{1}{4}$-cup), or a sum of unit and non-unit fractions ($\frac{1}{4}$+$\frac{1}{4}$+$\frac{3}{4}$, or adding $\frac{1}{4}$-cup twice and then adding one $\frac{3}{4}$-cup).
(IM K–5 Math: Grade 4 Unit 3 Lesson 7 Activity 1)
Later, number line diagrams, which in earlier grades supported students in reasoning about addition and subtraction of whole numbers, now support them in adding and subtracting fractions with the same denominator.
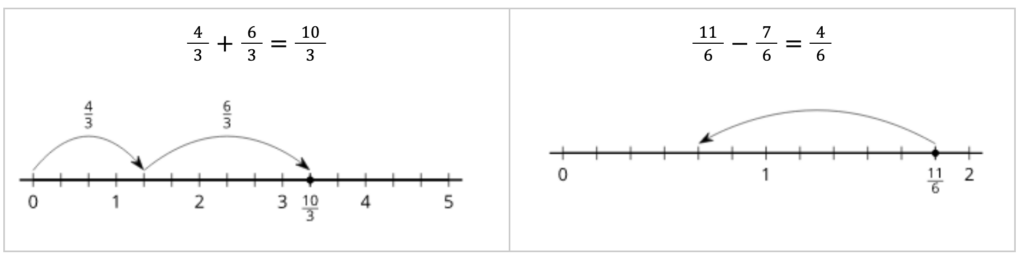
IM K–5 Math: Grade 4 Unit 3 Overview
This representation also helps students see that a fraction greater than 1 can be decomposed into a whole number and a fraction, and then be expressed as a mixed number.
Students rely on the understandings developed in Units 1 and 2 to write equivalent fractions in tenths and hundredths, and then find sums of tenths and hundredths. For instance, to find $\frac{3}{10}$+$\frac{15}{100}$, they reason that $\frac{3}{10}$ is equivalent to $\frac{30}{100}$, so the sum is $\frac{30}{100}$+$\frac{15}{100}$, which is $\frac{45}{100}$ (IM K–5 Math: Grade 4 Unit 3 Overview). The reasoning here paves the way for students to learn about decimal notation in the next unit.
Place Value, Purposefully Postponed
In earlier units, students began to develop a mental concept around tenths and hundredths. In Unit 4, they connect decimal fractions to numbers and place value in base ten.
Unit 4, From Hundredths to Hundred-thousands, begins with small numbers. Students learn about decimal notation, reason about the size of tenths and hundredths written as decimals, locate decimals on a number line, and compare and order them. They are prompted to notice the structure of the decimal notation and how it relates to place value.
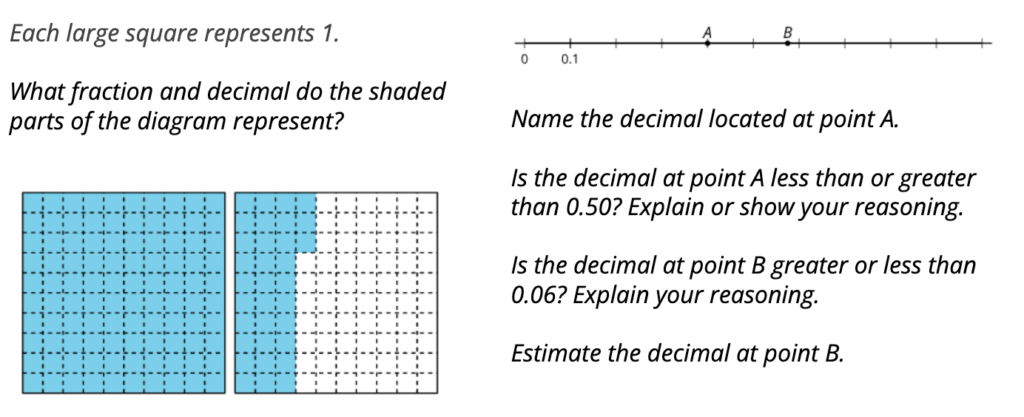
IM K–5 Math: Unit 4 Lesson 1 Activity 1
IM K–5 Math: Unit 4 Lesson 3 Activity 2
After attending to place value in small numbers, students shift their attention to place value in larger numbers. They use base-ten blocks and diagrams to build, read, write, and represent whole numbers beyond 1,000. Working with numbers within 1,000,000 is quite a leap from the incremental increases in the numbers being explored in kindergarten through grade 3 (such as working within 20, 100, or 1,000), but grade 4 students are ready and can generalize more broadly. They observe that ten-thousands are related to thousands in the same way that thousands are related to hundreds, and hundreds are to tens, and tens are to ones—each base-ten unit is 10 times the next smaller unit.
Multiplicative reasoning and the idea of multiples comes into play as students reason about the size of large numbers. Students use their observations of structure to compare, order, and round numbers (by thinking about multiples of 10, 100, 1,000, 10,000, and 100,000 that are the closest to the number).
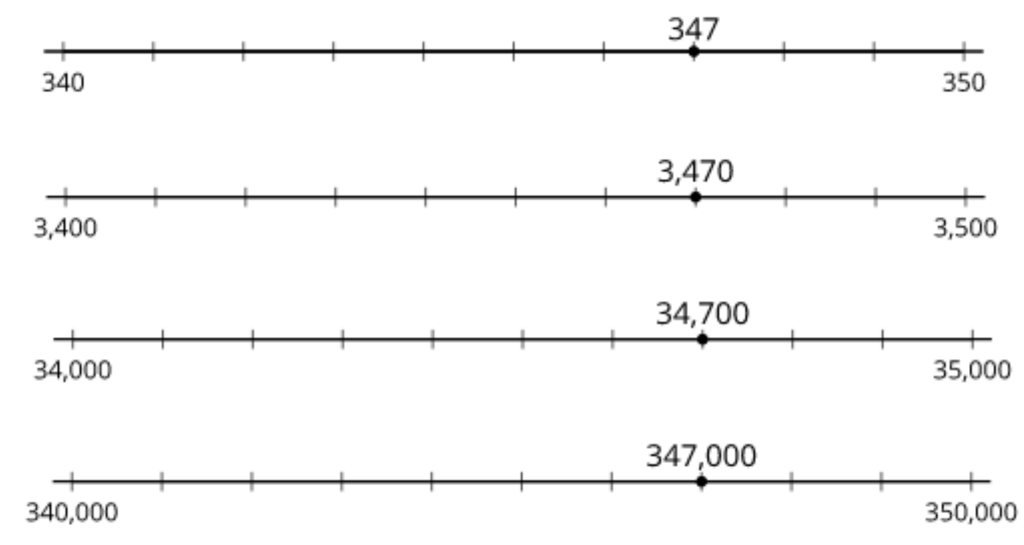
IM K–5 Math: Grade 4 Unit 4 Section B Overview
With a deeper understanding of place value, students are better prepared to consolidate their learning about addition and subtraction of whole numbers and to develop fluency as intended within the K–5 progression of addition and subtraction.
A Closer Look at Multiplication and Measurement
Unit 5, Multiplicative Comparison and Measurement, comes next. Since Unit 4 ends with addition and subtraction of multi-digit numbers, why not go right into multiplication and division of multi-digit numbers? This is because students would benefit from first developing deeper understandings around multiplication and division, measurement, and problem solving before venturing to learn ways to find products and quotients of larger numbers. In other words, the work in Unit 5 gives students better access to the major work of multiplying and dividing multi-digit numbers.
Up to this point, students have understood equal-size groups. Here, students make sense of multiplication as a way to compare quantities. In prior grades, they made additive comparisons, asking “how much more or less?” In multiplicative comparison, the key question is “how many times as much or as many?” Students use diagrams and equations to reason about situations that involve comparing multiplicatively.

IM K–5 Math: Grade 4 Unit 5 Overview and Section A Overview
Multiplicative comparison is also helpful in relating units of measurement. For instance, we generally think of 1 yard as 3 times as long as 1 foot, rather than as 2 feet longer than 1 foot. Solving problems that involve measurement conversion and fractional values, though classified as “supporting work” of the grade, also reinforces concepts on fractions and operations that are central in grade 4.
Upon their arrival in Unit 6, Multiplying and Dividing Multi-Digit Numbers, students are more ready for this major work of the grade. They can see the benefits of decomposing factors or dividends by place value, make sense of different representations—diagrams, equations, and algorithms—being used to organize partial products or partial quotients, and make connections between reasoning strategies and representations.

IM K–5 Math: Grade 4 Unit 6 Overview Sections B and C
Put another way, students are better equipped to notice and make use of structure—of base-ten numbers, properties of operations, and the relationship between multiplication and division—to multiply and divide larger numbers effectively and strategically. The progression of the work in Units 1–6 helps to put students on a pathway toward fluency with these operations as expected in their K–5 journey.
Next Steps
At first glance, the story of grade 4 may seem to follow a curious path. We hope that a closer look shows a coherent sequence that allows students to make stronger connections across topics and opens the access to grade-level work for a wider range of learners. We also invite your reflections.
- What other considerations may support the placement of multi-digit operations and place value work in this course?
- In what other ways might the design decisions improve students’ chance of reaching grade-level standards and empower them to know, use, and enjoy mathematics?
Check out the entire Stories of Grades K–5 blog post series:
Story of Kindergarten
Story of Grade 1
Story of Grade 2
Story of Grade 3
Story of Grade 4
Story of Grade 5
You can also download IM’s Stories of Grades K–5 free ebook!
