By Mike Henderson
Teaching addition and subtraction in grade 2 is a challenging balancing act. As students move from numbers within 100 to numbers within 1,000, they need to use approaches that involve directly representing the quantities they are adding or subtracting and be supported in reasoning more abstractly. However, we don’t want students to feel they always have to represent the quantities they add and subtract with objects or drawings, especially within 20. Although we want students to use increasingly abstract and efficient strategies based on place value, we don’t want to push them too fast toward the algorithms they will use in grades 3 and 4 or position these strategies as the “right” way to add or subtract.
When considering different ways to tell the mathematical story of grade 2, we wondered:
- How do we make sure students are given time to consolidate their understanding of numbers and operations within 100 before extending their place value understanding within 1,000?
- How do we make sure students spend time making sense of place value strategies without feeling forced to use procedures that do not make sense to them?
- How do we make sure students (and their teachers) do not feel pressure to master a laundry list of different strategies and representations for adding and subtracting?
We know students enter grade 2 with a variety of approaches for reasoning about adding and subtracting numbers. We want them to know that the ways they think about addition and subtraction continue to make sense even as the numbers get substantially larger. Although understanding place value and using place value understanding to add and subtract is the major work of the grade, a goal in writing the story of grade 2 was to make sure students focus on foundational math concepts without feeling funneled toward procedural ways of thinking.
The invitation to grade 2 math
The initial lessons of grade 2 invite students to learn more about each other and the ways they do math through activities and games that focus on addition and subtraction within 20. They continue to learn more about each other and their interests by asking questions and organizing data with picture graphs and bar graphs. The activities provide opportunities to build a joyful math community where students are encouraged to share ideas and celebrate different ways of thinking.
Teachers learn about the ways students think about addition and subtraction. An important focus in the early lessons is on combinations of 10 and making 10. These early activities help students not only recall their work with combinations of numbers that make 10 from kindergarten and grade 1, but also recall their work with place value. Later activities in the section give teachers an opportunity to learn about how students think about tens and ones as they represent numbers within 50 and add them.
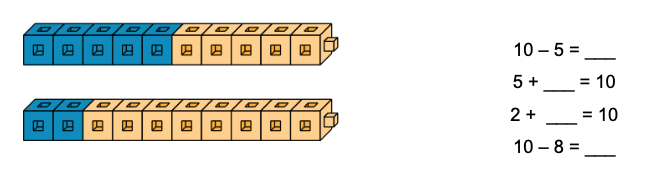
IM K–5 Math: Grade 2 Unit 1 Lesson 2 Activity 2
The picture graphs and bar graphs also provide an accessible way for students to show different ways they may add or subtract. As they answer questions about the graphs, students show different ways to add and compare quantities within 20, including strategies like counting on. Although counting strategies as students’ go-to method will fade throughout the year, it is a useful strategy that makes sense to many students and one we want students to continue to use with flexibility. The number range is intentionally kept within 20 in this section to make the work accessible to all students, while nudging students to reason more abstractly about the graphs.
Teachers also have opportunities to learn about how students add within 100 with a focus on how they think about adding using their understanding of place value. The numbers used are intentionally within 100 to give a purpose for introducing a more abstract representation to make sense of the quantities in Compare problems—the tape diagram. Although the tape diagram is not a representation used to make sense of performing computations, it does help students make sense of the relationships between quantities in story problems and apply what they know about the relationship between addition and subtraction to solve problems.
Subtract with strategies based on place value
Where Unit 1 elicits what students already know about addition and subtraction, Unit 2 extends their understanding of subtraction within 100 using strategies based on place value and other ways that make sense to them. Students build on counting strategies to consider how they might count on by tens and ones.

- Make trains with cubes.
- Find the total number of cubes you and your partner used. Show your thinking.
- Find the difference between the number of cubes you and your partner used. Show your thinking.
IM K–5 Math: Grade 2 Unit 2 Lesson 1 Activity 2
Students are then introduced to base-ten blocks as a way to represent tens and ones. Students explore these blocks and compare them to their use of connecting cubes. Although students may continue to use connecting cubes throughout the unit, as the numbers increase in size, they begin to see the benefit of using base-ten blocks to quickly show tens and ones.
IM K–5 Math: Grade 2 Unit 2 Lesson 2 Activity 1
This leads to more explicit conversations about place value. Students show their understanding of the value of each digit as they explain the ways they represent situations using base-ten blocks and expressions.

IM K–5 Math: Grade 2 Unit 2 Lesson 5 Activity 2
Students make sense of base-ten drawings. Students first see and use these drawings in grade 1 when they are a direct representation of the connecting cube towers of 10 and single cubes. Now, students may interpret them as connecting cubes or as base-ten blocks. Over the course of the year, students continue to use base-ten blocks and drawings to represent decomposing tens in different ways.
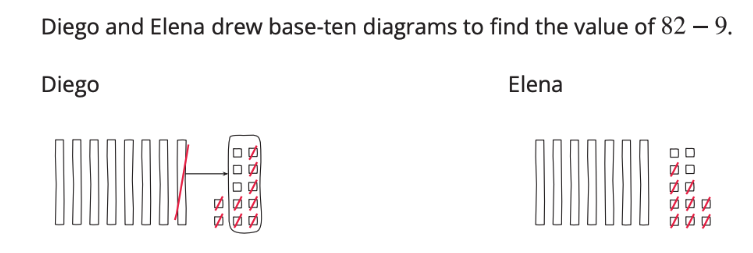
IM K–5 Math: Grade 2 Unit 2 Lesson 6 Activity 1
Although the unit introduces base-ten blocks and decomposing a ten as a strategy for subtraction within 100, both are built on ways students have reasoned about and represented operations with two-digit numbers in grade 1. Students are asked to make sense of and try out different ways to represent decomposing a ten when subtracting by place, but they are not expected to use one particular strategy or representation at the end of the Unit 2 to subtract. Students should continue to use the approaches that make sense to them.
Deep dives on length and a hundred
Length and the number line
In Unit 3, students extend their understanding of measuring length as they make sense of and use standard length units. Students measure, compare, and add lengths using a variety of concrete and abstract tools. This helps all students continue to consolidate their understanding of the structure of the number system and prepares them to make sense of the number line. Students’ understanding of length units and the way length units are represented on a ruler is essential to work with the number line for addition and subtraction in Unit 4 and lays a foundation for students’ understanding of fractions as numbers in grade 3.

In Unit 4, students continue to deepen their number sense within 100 as they locate numbers and reason about their relative size. They also use the number line to deepen their understanding of addition and subtraction. In particular, the number line helps students think about subtraction as the distance or length between two numbers on the number line. This understanding helps students flexibly choose computation strategies within 100 and decide when some strategies might be more useful than others. For example, compare these different approaches for finding 81 – 79 that students investigate in Unit 7 Lesson 1.
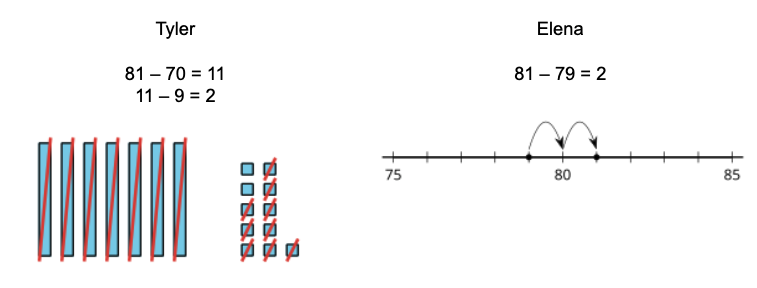
IM K–5 Math: Grade 2 Unit 7 Lesson 1 Activity 1
Although the number line is not a representation that easily shows composing or decomposing base-ten units, it does help students show and explain strategies based on counting on or counting back by place. Students also see the strategies they used when adding and subtracting within 20—such as making or getting to a multiple of 10—continue to work with larger numbers.
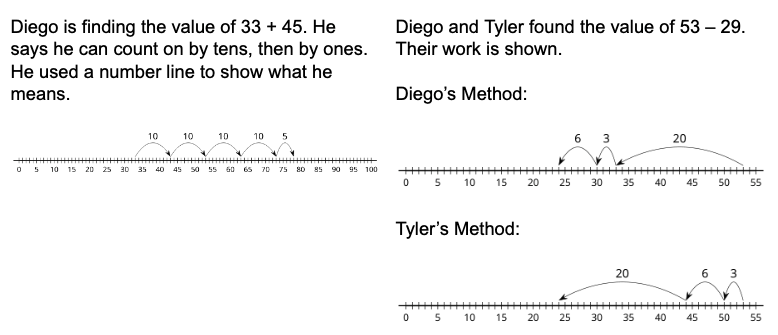
IM K-5 Math: Grade 2 Unit 4 Lesson 10 Activity 2 and Unit 4 Lesson 11 Activity 1
A hundred
In Unit 5 students make sense of a hundred as a base-ten unit.
Finally! Three-digit numbers and place value! Many teachers may recognize the content of this unit as the traditional focus of early units of grade 2. Although we know that many students are ready to extend their understanding of place value to include a hundred at the beginning of grade 2, we also believe that in building on students’ understanding and strengths with working within 100 in earlier units, all students will be able to make sense of a hundred as a unit and will be less likely to feel like strategies based on place value are the only (or “right”) ways to add and subtract.
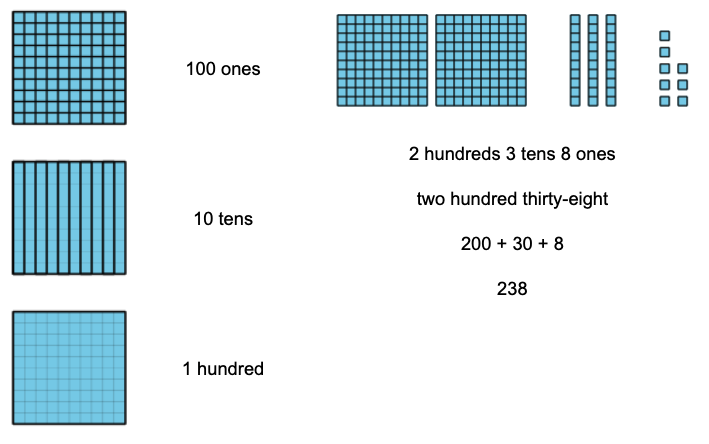
IM K–5 Math: Grade 2 Unit 5 Section A Overview
Because the introduction of three-digit numbers comes after extensive work with numbers on the number line, students are also able to use this tool as a way to compare three-digit numbers. Although the focus in the unit is on using place value reasoning to compare numbers, the number line supports students’ ongoing development of number sense and counting within 1,000. The development of a strong sense of the relative size of three-digit numbers helps later when students consider the relationship between numbers in an expression before selecting the approach for finding its value.

How do both representations show that 432 > 423? How does each representation connect to students’ development of strategies for addition and subtraction within 1,000?
Adapted from IM K–5 Math: Grade 2 Unit 5 Lesson 9 Activity 2
Consolidation
In Units 6, 7, and 8, students consolidate their understanding about addition and subtraction within 100 and their understanding of place value within 1,000. In Unit 6, students extend their understanding of number lines and skip-counting to tell time to the nearest hour and minute on analog clocks. They also add and subtract within 100 as they solve problems with money. In Unit 8, students skip-count and use expressions with equal addends to determine whether quantities are even or odd, and to find the total number of objects in an array. This is the foundation for their work with multiplication in grade 3.
In Unit 7, students add and subtract within 1,000. No new strategies or representations are introduced in this unit. Students build on the ways they have added and subtracted numbers since Unit 1 with the ways they represented numbers within 1,000 in Unit 4. This includes inviting students to think about ways they can use the relationship between addition and subtraction and counting on strategies.
They make sense of ways to compose and decompose units, and explore different ways to represent their thinking. No one approach is positioned as the “right” way to add or subtract by place, and the emphasis is intentionally on place value concepts rather than procedures to avoid moving too fast toward the standard algorithm.
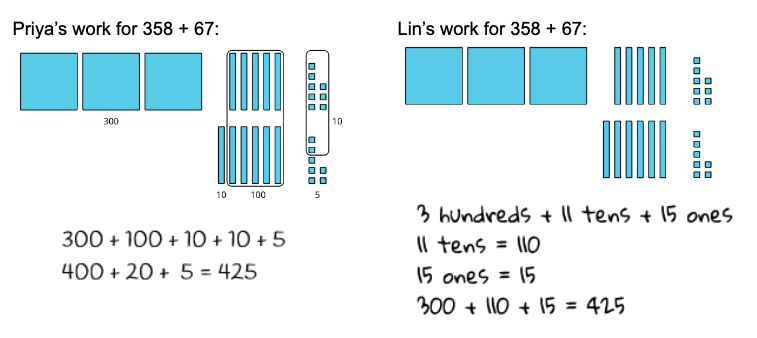
IM K–5 Math: Grade 2 Unit 7 Lesson 8 Activity 2
The unit lays a foundation for understanding and using algorithms in later grades. For example, the way we present drawings to students in the materials mirrors the annotation used in many subtraction algorithms.
Mai used base-ten blocks to find the value of 336 – 52. Then, she started making a diagram to show her work.
Explain what Mai did in Step 2. Show what Mai could do next to find the difference.

IM K–5 Math: Grade 2 Unit 7 Lesson 16 Activity 1
Students also see recording methods that are precursors to the algorithms they will see in grade 3 and build off the ways they represented three-digit numbers in Unit 4. However, they are not expected to use or master these recording methods. The mathematical purpose is for students to make sense of these methods and to invite students to try them. They connect the ways that make sense to them to these more abstract recording methods. They also have opportunities throughout the unit to share their own thinking, including any invented algorithms, and reflect on ways to make their thinking clear for themselves and others.
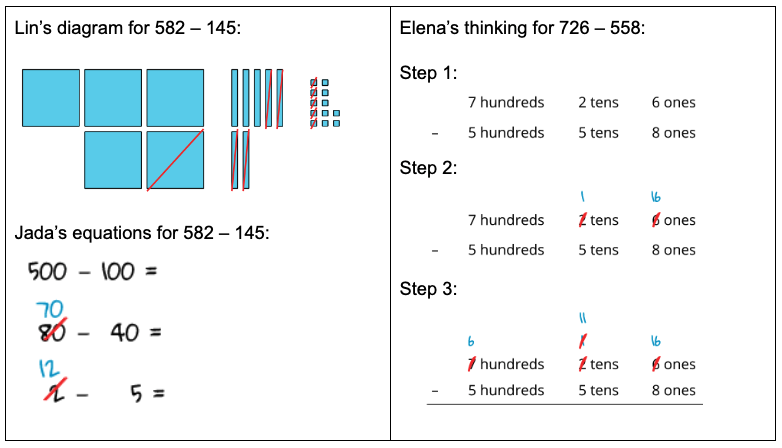
IM K–5 Math: Grade 2 Unit 7 Lesson 15 Activity 1
Throughout each section of the unit, students flexibly choose strategies and explain why they chose a particular strategy based on the numbers in the expressions. They continue to see that the strategies they learned in earlier grades continue to work with larger numbers.
Jada’s thinking for 402 – 298
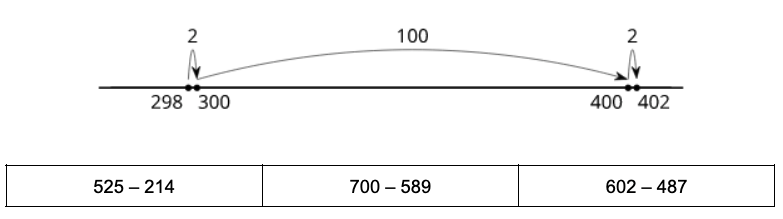
What ways might you expect students to find the value of these differences? How might they show that they are thinking about the relationship between the numbers and choosing strategies flexibly and strategically? How do these strategies connect to the strategies they shared as early as Unit 1?
IM K–5 Math: Grade 2 Unit 7 Lesson 16
Next Steps
From the beginning of grade 2, students use the approaches that make sense to them as they add and subtract within 100. They are introduced to a limited selection of new representations—base-ten blocks and number lines—as ways to represent their operational thinking. Each strategy they use is an extension of strategies they have used before with smaller numbers. How do these choices in our story help students develop an understanding that math makes sense? How does it prepare students for the work of adding and subtracting with algorithms in grade 3 and the standard algorithm in grade 4?
Check out the entire Stories of Grades K–5 blog post series:
Story of Kindergarten
Story of Grade 1
Story of Grade 2
Story of Grade 3
Story of Grade 4
Story of Grade 5
You can also download IM’s Stories of Grades K–5 free ebook!
