By Vanessa Cerrahoglu and Danielle Seabold, IM Certified® Facilitators
Learners have brilliant mathematical ideas. How we teachers use IM 6–12 Math™ impacts how often students and teachers recognize this brilliance.
“…[C]urriculum choices matter. But how teachers use curriculum matters even more.”
EdReports, State of the Instructional Materials Market 2020.
Illustrative Mathematics (IM) believes that each student is the author of brilliant mathematical ideas. For this reason, IM built a problem-based curriculum where students listen, respond to, and value each other’s thinking as they continue their journey in becoming powerful doers of mathematics.
This post is the second in a series of three in which we seek to:
- Highlight instructional opportunities teachers have within IM 6–12 Math™ to enhance access students have to the mathematical content. You can read more in Leveraging IM 6–12 Math Teacher Materials to Enhance Access to Grade-Level Mathematics.
- Reflect with teachers and identify additional opportunities to enhance access and challenge within IM 6–12 Math™ based on students’ strengths.
- Describe a process teachers can use to prepare and plan for an upcoming lesson with access in mind.
We look forward to hearing from you about what resonates with your own experiences and how this series may inform your practice moving forward.
Learners have brilliant mathematical ideas. These sparks of brilliance, once ignited, lead learners down a pathway towards becoming expert learners. Expert learners recognize their own brilliant ideas and share them with others, to enhance learning within the mathematical classroom community. However, sometimes things get in the way of students and teachers noticing the sparks.
In our previous post, Leveraging IM 6–12 Math Teacher Materials to Enhance Access to Grade-Level Mathematics, we highlighted one vehicle for noticing brilliance. These strategies, embedded in the curriculum, are informed by the Universal Design for Learning. With enhanced access, students can excel with grade-level mathematics. The more we understand these opportunities, the more we notice and use them. Here, we highlight ways we teachers can leverage our own expertise and knowledge of our students (and their strengths) to create a space for students to become expert learners.
What do we mean by expert learners? Expert learners are motivated, resourceful, and strategic. (The UDL Guidelines) They rely on multiple ways to engage with, represent, and communicate mathematical thinking and ideas. This means that their mathematical ideas may come out looking and sounding like something quite different than what we may have anticipated. It’s in these very moments where we teachers have the opportunity to slow down and look closely to provide kindling to further ignite the spark.
Let’s take Grade 7 Unit 6 Lesson 18: Subtraction in Equivalent Expressions for example. The learning goals of this lesson are:
- Explain (orally, in writing, and using other representations) how the distributive and commutative properties apply to expressions with negative coefficients.
- Justify (orally and in writing) whether expressions are equivalent, including rewriting subtraction as adding the opposite.
As they work towards these learning goals, students will engage with multiple forms of mathematical expressions—algebraic and visual—and articulate connections between equivalent forms of an expression using the distributive property.
In the first two activities of the lesson, students have an opportunity to ground themselves by examining ways of working with signed numbers. In Activity 2: A Helpful Observation, students recall that subtracting a number (or expression) is equivalent to adding its additive inverse. Making this concept explicit through a numeric example opens the door for students to see the usefulness of working with the additive inverse when they come to justify why
$7\frac34+3\frac56-1\frac34$ is equivalent to $7\frac34+\text-1\frac34+3\frac56$
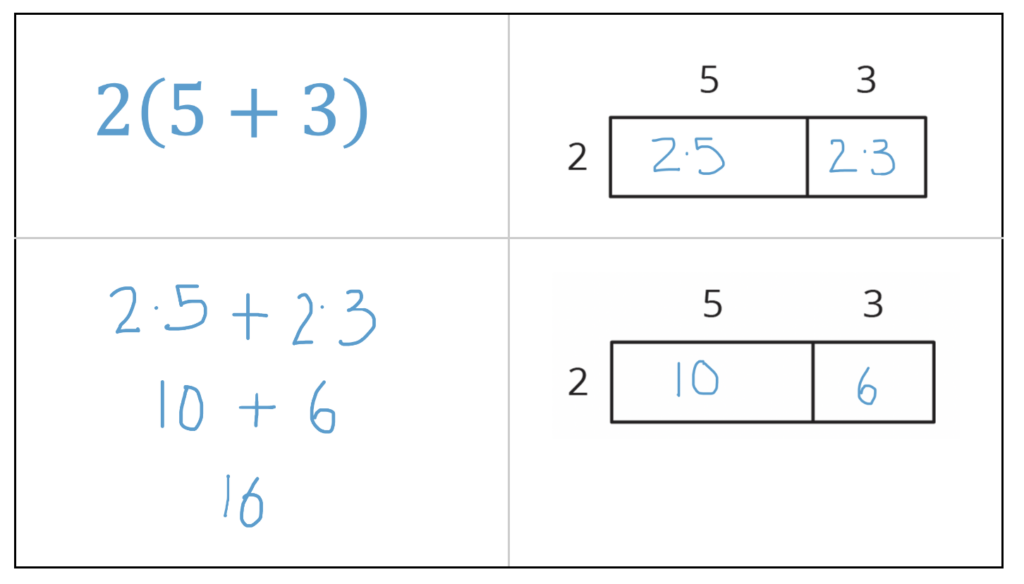
In Activity 3: Organizing Work, students build on previous understandings, including work with tape diagrams and equations.

Students connect rewriting subtraction expressions with previous work about the distributive property. They are also transitioning from concrete diagrams that represent area to abstract diagrams that are no longer about area (because of the negative numbers). The abstract diagrams become a way to represent and organize their thinking and work.
Students are doing important mathematical work focused on conceptual processing. As a result, there is an embedded suggested strategy to enhance the access students have to the math.

So, how might we begin with an example with more accessible values? In this case, the authors have done some of the heavy lifting for teachers by suggesting an activity launch to serve this purpose.

When brought to life, the suggested instructional move may result in a collection of student work that may look something like this:
Analyzing these four work samples makes space for students to engage in a conversation with each other. When students work to compare and connect different ways of representing thinking about this prompt they leverage cognitive strengths such as language or visual-spatial processing.
The suggested instructional move for providing access for English learners is the use of Math Language Routine 7 (MLR7): Compare and Connect as described below.

In leveraging the suggested instructional moves, the launch, and also MLR7, we have an opportunity to move the learning forward with all students at the start of an activity. Some may wonder about how to keep the momentum moving when students get to question 3 of Activity 18.3: Organizing Work: Use the distributive property to write an expression that is equivalent to $\frac12(8y-x-12)$. Upon the first read, one might infer there’s a bias towards algebraic representation, and some may argue the push comes too soon.
Perhaps this is a place where teachers may lean into the UDL framework and hold space for students to “take risks, ask questions, and be honored for being themselves” (Fritzgerald). We can encourage students to tap into their cognitive strengths and use strategies and tools from earlier in the lesson, even when not called for explicitly within the material. In doing so, we may see students draw a tape diagram to represent this expression or we may see students engage in a back-and-forth conversation with classmates. It is in these spaces that students become expert learners. They may try on different avenues of engagement, representation, and action and expression until they find the means that work best for them for the given context. And they do so in community with their peers.
As students work on these prompts, the classroom teacher may monitor and select varied student responses to amplify different ways of knowing, doing, and being in mathematics.
Next Steps
As you prepare for an upcoming lesson, we invite you to
- anticipate various ways students may respond to a prompt
- identify connections between the anticipated methods and cognitive functions
- consider your students’ cognitive strengths:
- How might you leverage students’ strengths to overcome possible barriers?
- What additional instructional moves, suggested within the curriculum or from your own experience, might make space for students to learn to become expert learners?
- How will you use these insights to bring the lesson to life?
Please be on the lookout for the next post in this series, and share insights gained by going through this process. We’d love to learn from you.
Resources Cited
Fritzgerald, Andratesha. “Antiracism and Universal Design for Learning: Building Expressways to Students.” CAST, 2020.
https://poorvucenter.yale.edu/LearningStylesMyth
https://journals.sagepub.com/doi/full/10.1177/1477878515606621
https://eric.ed.gov/?id=EJ896354
https://www.tandfonline.com/doi/abs/10.1080/00091383.2010.503139?journalCode=vchn20
